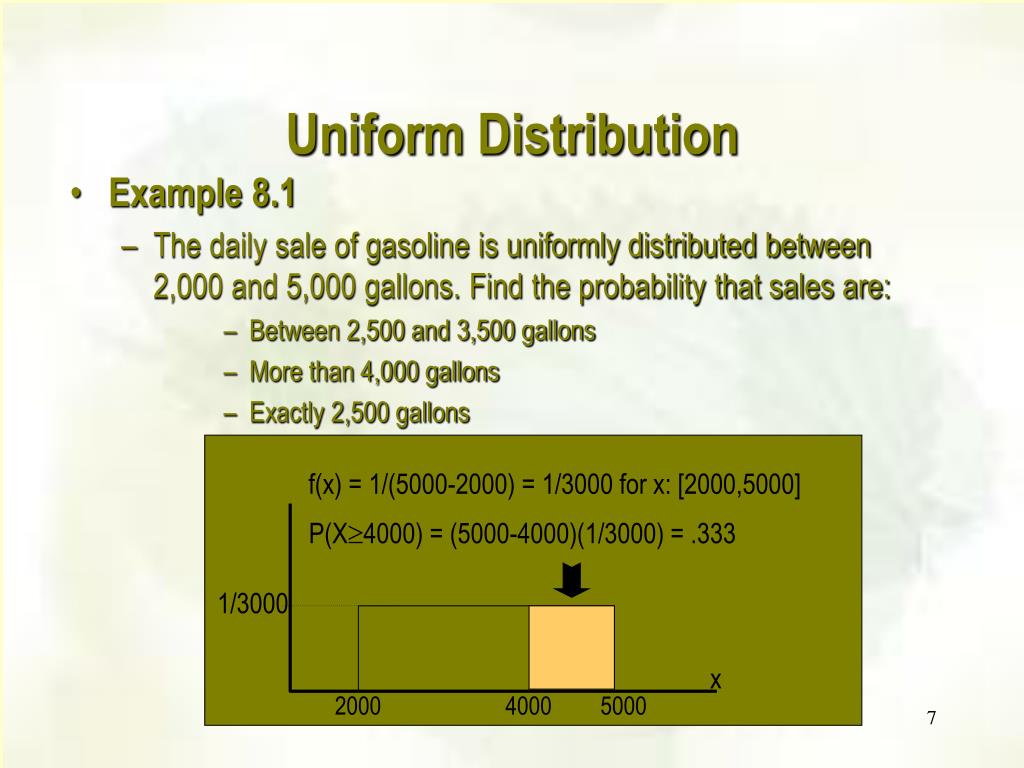
Uniform Distribution Plus Constant . Suppose i have a random variable $x$ and to this, i add a constant $c>0$. Let its support be a closed interval of real numbers: Definition let be a continuous random variable. A continuous random variable x has a uniform distribution, denoted u ( a, b), if its probability density function is: The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to. The uniform distribution assigns equal probabilities to intervals of equal lengths, since it is a constant function, on the interval it is non. The \(p^{th}\) percentile of the uniform distribution is calculated by using linear interpolation: Will $x+c$ have a different distribution? We say that has a uniform distribution on the interval if and only if its.
from www.slideserve.com
Let its support be a closed interval of real numbers: The uniform distribution assigns equal probabilities to intervals of equal lengths, since it is a constant function, on the interval it is non. Definition let be a continuous random variable. We say that has a uniform distribution on the interval if and only if its. Will $x+c$ have a different distribution? The \(p^{th}\) percentile of the uniform distribution is calculated by using linear interpolation: The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to. Suppose i have a random variable $x$ and to this, i add a constant $c>0$. A continuous random variable x has a uniform distribution, denoted u ( a, b), if its probability density function is:
PPT Continuous Probability Distributions PowerPoint Presentation
Uniform Distribution Plus Constant Will $x+c$ have a different distribution? Let its support be a closed interval of real numbers: Will $x+c$ have a different distribution? We say that has a uniform distribution on the interval if and only if its. Definition let be a continuous random variable. A continuous random variable x has a uniform distribution, denoted u ( a, b), if its probability density function is: The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to. The \(p^{th}\) percentile of the uniform distribution is calculated by using linear interpolation: Suppose i have a random variable $x$ and to this, i add a constant $c>0$. The uniform distribution assigns equal probabilities to intervals of equal lengths, since it is a constant function, on the interval it is non.
From www.slideserve.com
PPT Uniform Distribution PowerPoint Presentation, free download ID Uniform Distribution Plus Constant Will $x+c$ have a different distribution? The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to. The \(p^{th}\) percentile of the uniform distribution is calculated by using linear interpolation: Let its support be a closed interval of real numbers: We say that has a uniform distribution on the interval if and only. Uniform Distribution Plus Constant.
From www.cuemath.com
Uniform Distribution Formula Learn the Uniform Distribution Formula Uniform Distribution Plus Constant Definition let be a continuous random variable. We say that has a uniform distribution on the interval if and only if its. The \(p^{th}\) percentile of the uniform distribution is calculated by using linear interpolation: The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to. Let its support be a closed interval. Uniform Distribution Plus Constant.
From studylib.net
1 Uniform Distribution Uniform Distribution Plus Constant Let its support be a closed interval of real numbers: The uniform distribution assigns equal probabilities to intervals of equal lengths, since it is a constant function, on the interval it is non. A continuous random variable x has a uniform distribution, denoted u ( a, b), if its probability density function is: Suppose i have a random variable $x$. Uniform Distribution Plus Constant.
From www.slideserve.com
PPT Simulation of Uniform Distribution on Surfaces PowerPoint Uniform Distribution Plus Constant We say that has a uniform distribution on the interval if and only if its. Will $x+c$ have a different distribution? The uniform distribution assigns equal probabilities to intervals of equal lengths, since it is a constant function, on the interval it is non. Definition let be a continuous random variable. The \(p^{th}\) percentile of the uniform distribution is calculated. Uniform Distribution Plus Constant.
From www.researchgate.net
Figure Uniform Distribution. Figure Gaussian Distribution Uniform Distribution Plus Constant We say that has a uniform distribution on the interval if and only if its. Let its support be a closed interval of real numbers: Will $x+c$ have a different distribution? Definition let be a continuous random variable. The \(p^{th}\) percentile of the uniform distribution is calculated by using linear interpolation: The uniform distribution is a continuous probability distribution and. Uniform Distribution Plus Constant.
From www.pinterest.com
Uniform Distribution Uniform distribution, Math, Statistics Uniform Distribution Plus Constant Let its support be a closed interval of real numbers: We say that has a uniform distribution on the interval if and only if its. Will $x+c$ have a different distribution? Definition let be a continuous random variable. The uniform distribution assigns equal probabilities to intervals of equal lengths, since it is a constant function, on the interval it is. Uniform Distribution Plus Constant.
From necolnassima.blogspot.com
43+ continuous uniform distribution calculator NecolNassima Uniform Distribution Plus Constant Let its support be a closed interval of real numbers: The uniform distribution assigns equal probabilities to intervals of equal lengths, since it is a constant function, on the interval it is non. The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to. Suppose i have a random variable $x$ and to. Uniform Distribution Plus Constant.
From www.slideserve.com
PPT Continuous Probability Distributions PowerPoint Presentation Uniform Distribution Plus Constant Definition let be a continuous random variable. Will $x+c$ have a different distribution? The \(p^{th}\) percentile of the uniform distribution is calculated by using linear interpolation: A continuous random variable x has a uniform distribution, denoted u ( a, b), if its probability density function is: The uniform distribution assigns equal probabilities to intervals of equal lengths, since it is. Uniform Distribution Plus Constant.
From www.slideshare.net
Uniform Distribution Uniform Distribution Plus Constant Let its support be a closed interval of real numbers: The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to. Suppose i have a random variable $x$ and to this, i add a constant $c>0$. The \(p^{th}\) percentile of the uniform distribution is calculated by using linear interpolation: A continuous random variable. Uniform Distribution Plus Constant.
From medium.com
Probability distributions used in machine learning (part 1) by Peter Uniform Distribution Plus Constant Will $x+c$ have a different distribution? Suppose i have a random variable $x$ and to this, i add a constant $c>0$. The uniform distribution assigns equal probabilities to intervals of equal lengths, since it is a constant function, on the interval it is non. We say that has a uniform distribution on the interval if and only if its. Let. Uniform Distribution Plus Constant.
From analystprep.com
Continuous Unifrom Distribution Example CFA Level 1 AnalystPrep Uniform Distribution Plus Constant Will $x+c$ have a different distribution? The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to. The uniform distribution assigns equal probabilities to intervals of equal lengths, since it is a constant function, on the interval it is non. The \(p^{th}\) percentile of the uniform distribution is calculated by using linear interpolation:. Uniform Distribution Plus Constant.
From enjoymachinelearning.com
Machine Learning 101 Normal Distribution Vs Uniform Distribution » EML Uniform Distribution Plus Constant Suppose i have a random variable $x$ and to this, i add a constant $c>0$. We say that has a uniform distribution on the interval if and only if its. Will $x+c$ have a different distribution? A continuous random variable x has a uniform distribution, denoted u ( a, b), if its probability density function is: The uniform distribution assigns. Uniform Distribution Plus Constant.
From www.slideserve.com
PPT Continuous Probability Distributions PowerPoint Presentation Uniform Distribution Plus Constant Let its support be a closed interval of real numbers: Will $x+c$ have a different distribution? We say that has a uniform distribution on the interval if and only if its. The uniform distribution assigns equal probabilities to intervals of equal lengths, since it is a constant function, on the interval it is non. Suppose i have a random variable. Uniform Distribution Plus Constant.
From uqtestfuns.readthedocs.io
Uniform Distribution — UQTestFuns Uniform Distribution Plus Constant Let its support be a closed interval of real numbers: A continuous random variable x has a uniform distribution, denoted u ( a, b), if its probability density function is: The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to. Suppose i have a random variable $x$ and to this, i add. Uniform Distribution Plus Constant.
From ar.inspiredpencil.com
Uniform Distribution Uniform Distribution Plus Constant Let its support be a closed interval of real numbers: Will $x+c$ have a different distribution? Definition let be a continuous random variable. A continuous random variable x has a uniform distribution, denoted u ( a, b), if its probability density function is: Suppose i have a random variable $x$ and to this, i add a constant $c>0$. The uniform. Uniform Distribution Plus Constant.
From www.youtube.com
Uniform distribution (discrete) YouTube Uniform Distribution Plus Constant The uniform distribution assigns equal probabilities to intervals of equal lengths, since it is a constant function, on the interval it is non. We say that has a uniform distribution on the interval if and only if its. Let its support be a closed interval of real numbers: Definition let be a continuous random variable. Will $x+c$ have a different. Uniform Distribution Plus Constant.
From www.home-tution.com
Uniform Distribution Formula Theory, Short Notes & Solved Examples Uniform Distribution Plus Constant The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to. A continuous random variable x has a uniform distribution, denoted u ( a, b), if its probability density function is: We say that has a uniform distribution on the interval if and only if its. Will $x+c$ have a different distribution? The. Uniform Distribution Plus Constant.
From andymath.com
Uniform Distribution Uniform Distribution Plus Constant The uniform distribution assigns equal probabilities to intervals of equal lengths, since it is a constant function, on the interval it is non. We say that has a uniform distribution on the interval if and only if its. Will $x+c$ have a different distribution? The uniform distribution is a continuous probability distribution and is concerned with events that are equally. Uniform Distribution Plus Constant.